NCERT Solutions for Class 7 Maths Chapter 4 on Simple Equations are available here. We have created step-by-step solutions with detailed explanations for those students who find it difficult to solve the comprehensive and intricate NCERT Solutions for Class 7 Maths. We recommend that students who aim to obtain high scores in Maths should refer to these solutions and enhance their understanding.
The NCERT Solutions for Class 7 Maths Chapter 4 – Simple Equations include 4 exercises that cover significant topics as Variable, Equation, Solving an Equation, Forming an Equation, Application of Simple Equations to Practical Situations
Simple Equations Key Points to remember
What is an Equation:
An equation is a statement of equality, which contains one or more unknown quantities or variables. It means that an equation is a statement that two expressions are equal.
For example, the equation x + 2 = 4 states that the expression x + 2 is equal to the expression 4.
NCERT Definition: The equality that involves variables is an equation.
Simple Linear Equation
An equation involving only a linear polynomial and which can be expressed in the form ax + b = 0, where a ≠ 0, is called a simple linear equation in one variable x.
A simple linear equation may be two variables also in the standard form that looks like this: Ax + By = C, where: A, B and C are coefficients (numbers) while x and y are variables.
- (i) A linear equation remains the same when the expression in the left and right are interchanged.
- (ii) In an equation, there is always an equality sign.
- (iii) Values on LHS and RHS are equal
Solution of a linear equation:
The value of the variable, which makes the equation a true statement is called the solution or root of a linear equation.
e.g., 5x – 12 = – 2 is an equation.
If x = 2, then LHS = 5x – 12 = 5 × 2 – 12 = 10 – 12 = – 2
LHS = RHS
Trial and error method of Solving Equations:
In trial-and-error method, putting the different values for the variables 0, 1, 2, 3,… one by one and then find
the corresponding values of LHS and RHS.
The value of variable, for which LHS = RHS, will be the solution of the linear equation.
Rules for solving an equation:
- (a) The same quantity can be added to both sides of an equation without changing the equality.
- (b) The same quantity can be subtracted from both sides of an equation without changing the equality.
- (c) Both sides of an equation may be multiplied by the same non-zero number without changing the equality.
- (d) Both sides of an equation may be divided by the same non-zero number without changing the equality.
Transposition of Terms:
Any term of an equation may be taken from one side to the other with a change in its sign. This does not affect the equality of the statement and this process is called transposition.
Class 7 Chapter 4 – Simple Equations NCERT Solutions
Exercise 4.1
1. Complete the last column of the table.
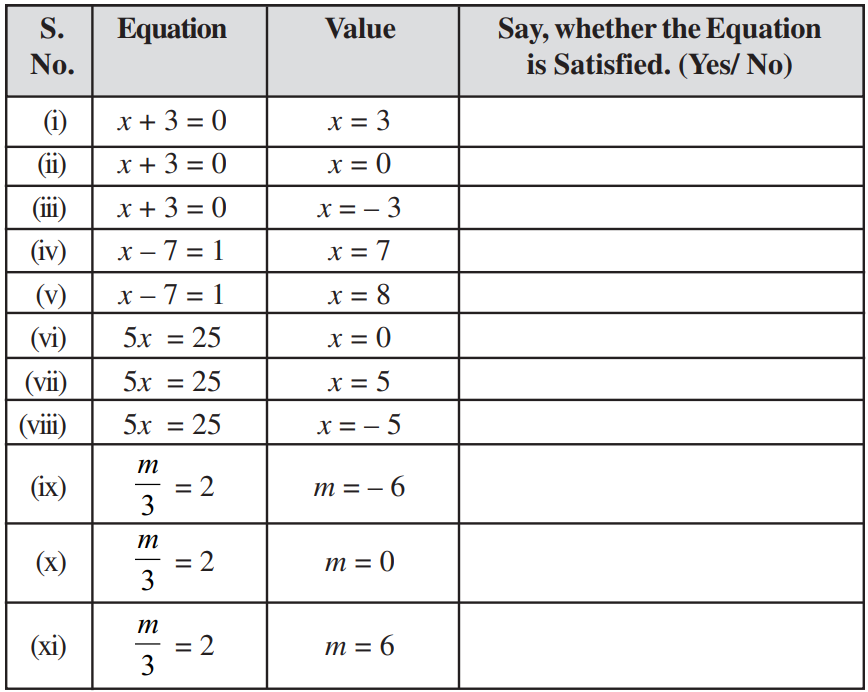
Solution:
(i) x + 3 = 0
LHS = x + 3
By substituting the value of x = 3
Then,
LHS = 3 + 3 = 6
By comparing LHS and RHS,
LHS ≠ RHS
∴ No, the equation is not satisfied.
(ii) x + 3 = 0
LHS = x + 3
By substituting the value of x = 0,
Then,
LHS = 0 + 3 = 3
By comparing LHS and RHS,
LHS ≠ RHS
∴ No, the equation is not satisfied.
(iii) x + 3 = 0
LHS = x + 3
By substituting the value of x = – 3,
Then,
LHS = – 3 + 3 = 0
By comparing LHS and RHS,
LHS = RHS
∴ Yes, the equation is satisfied.
(iv) x – 7 = 1
LHS = x – 7
By substituting the value of x = 7,
Then,
LHS = 7 – 7 = 0
By comparing LHS and RHS,
LHS ≠ RHS
∴ No, the equation is not satisfied.
(v) x – 7 = 1
LHS = x – 7
By substituting the value of x = 8,
Then,
LHS = 8 – 7 = 1
By comparing LHS and RHS,
LHS = RHS
∴ Yes, the equation is satisfied.
(vi) 5x = 25
LHS = 5x
By substituting the value of x = 0,
Then,
LHS = 5 × 0 = 0
By comparing LHS and RHS,
LHS ≠ RHS
∴ No, the equation is not satisfied.
(vii) 5x = 25
LHS = 5x
By substituting the value of x = 5,
Then,
LHS = 5 × 5 = 25
By comparing LHS and RHS,
LHS = RHS
∴ Yes, the equation is satisfied.
(viii) 5x = 25
LHS = 5x
By substituting the value of x = -5,
Then,
LHS = 5 × (-5) = – 25
By comparing LHS and RHS,
LHS ≠ RHS
∴ No, the equation is not satisfied.
(ix) m/3 = 2
LHS = m/3
By substituting the value of m = – 6,
Then,
LHS = -6/3 = – 2
By comparing LHS and RHS,
LHS ≠ RHS
∴ No, the equation is not satisfied.
(x) m/3 = 2
LHS = m/3
By substituting the value of m = 0,
Then,
LHS = 0/3 = 0
By comparing LHS and RHS,
LHS ≠ RHS
∴ No, the equation is not satisfied.
(xi) m/3 = 2
LHS = m/3
By substituting the value of m = 6,
Then,
LHS = 6/3 = 2
By comparing LHS and RHS,
LHS = RHS
∴ Yes, the equation is satisfied.
| S. No. | Equation | Value | Say whether the equation is satisfied. (Yes/No) |
| (i) | x + 3 = 0 | x = 3 | No |
| (ii) | x + 3 = 0 | x = 0 | No |
| (iii) | x + 3 = 0 | x = -3 | Yes |
| (iv) | x – 7 = 1 | x = 7 | No |
| (v) | x – 7 = 1 | x = 8 | Yes |
| (vi) | 5x = 25 | x = 0 | No |
| (vii) | 5x = 25 | x = 5 | Yes |
| (viii) | 5x = 25 | x = -5 | No |
| (ix) | (m/3) = 2 | m = – 6 | No |
| (x) | (m/3) = 2 | m = 0 | No |
| (xi) | (m/3) = 2 | m = 6 | Yes |
2. Check whether the value given in the brackets is a solution to the given equation or not.
(a) n + 5 = 19 (n = 1)
Solution:
LHS = n + 5
By substituting the value of n = 1,
Then,
LHS = n + 5
= 1 + 5
= 6
By comparing LHS and RHS,
6 ≠ 19
LHS ≠ RHS
Hence, the value of n = 1 is not a solution to the given equation n + 5 = 19.
(b) 7n + 5 = 19 (n = – 2)
Solution:
LHS = 7n + 5
By substituting the value of n = -2,
Then,
LHS = 7n + 5
= (7 × (-2)) + 5
= – 14 + 5
= – 9
By comparing LHS and RHS,
-9 ≠ 19
LHS ≠ RHS
Hence, the value of n = -2 is not a solution to the given equation 7n + 5 = 19.
(c) 7n + 5 = 19 (n = 2)
Solution:
LHS = 7n + 5
By substituting the value of n = 2,
Then,
LHS = 7n + 5
= (7 × (2)) + 5
= 14 + 5
= 19
By comparing LHS and RHS,
19 = 19
LHS = RHS
Hence, the value of n = 2 is a solution to the given equation 7n + 5 = 19.
(d) 4p – 3 = 13 (p = 1)
Solution:
LHS = 4p – 3
By substituting the value of p = 1,
Then,
LHS = 4p – 3
= (4 × 1) – 3
= 4 – 3
= 1
By comparing LHS and RHS,
1 ≠ 13
LHS ≠ RHS
Hence, the value of p = 1 is not a solution to the given equation 4p – 3 = 13.
(e) 4p – 3 = 13 (p = – 4)
Solution:
LHS = 4p – 3
By substituting the value of p = – 4,
Then,
LHS = 4p – 3
= (4 × (-4)) – 3
= -16 – 3
= -19
By comparing LHS and RHS,
-19 ≠ 13
LHS ≠ RHS
Hence, the value of p = -4 is not a solution to the given equation: 4p – 3 = 13.
(f) 4p – 3 = 13 (p = 0)
Solution:
LHS = 4p – 3
By substituting the value of p = 0,
Then,
LHS = 4p – 3
= (4 × 0) – 3
= 0 – 3
= -3
By comparing LHS and RHS,
– 3 ≠ 13
LHS ≠ RHS
Hence, the value of p = 0 is not a solution to the given equation 4p – 3 = 13.
3. Solve the following equations by trial-and-error method.
(i) 5p + 2 = 17
Solution:
LHS = 5p + 2
By substituting the value of p = 0,
Then,
LHS = 5p + 2
= (5 × 0) + 2
= 0 + 2
= 2
By comparing LHS and RHS,
2 ≠ 17
LHS ≠ RHS
Hence, the value of p = 0 is not a solution to the given equation.
Let, p = 1
LHS = 5p + 2
= (5 × 1) + 2
= 5 + 2
= 7
By comparing LHS and RHS,
7 ≠ 17
LHS ≠ RHS
Hence, the value of p = 1 is not a solution to the given equation.
Let, p = 2
LHS = 5p + 2
= (5 × 2) + 2
= 10 + 2
= 12
By comparing LHS and RHS,
12 ≠ 17
LHS ≠ RHS
Hence, the value of p = 2 is not a solution to the given equation.
Let, p = 3
LHS = 5p + 2
= (5 × 3) + 2
= 15 + 2
= 17
By comparing LHS and RHS,
17 = 17
LHS = RHS
Hence, the value of p = 3 is a solution to the given equation.
(ii) 3m – 14 = 4
Solution:
LHS = 3m – 14
By substituting the value of m = 3,
Then,
LHS = 3m – 14
= (3 × 3) – 14
= 9 – 14
= – 5
By comparing LHS and RHS,
-5 ≠ 4
LHS ≠ RHS
Hence, the value of m = 3 is not a solution to the given equation.
Let, m = 4
LHS = 3m – 14
= (3 × 4) – 14
= 12 – 14
= – 2
By comparing LHS and RHS,
-2 ≠ 4
LHS ≠ RHS
Hence, the value of m = 4 is not a solution to the given equation.
Let, m = 5
LHS = 3m – 14
= (3 × 5) – 14
= 15 – 14
= 1
By comparing LHS and RHS,
1 ≠ 4
LHS ≠ RHS
Hence, the value of m = 5 is not a solution to the given equation.
Let, m = 6
LHS = 3m – 14
= (3 × 6) – 14
= 18 – 14
= 4
By comparing LHS and RHS,
4 = 4
LHS = RHS
Hence, the value of m = 6 is a solution to the given equation.
4. Write equations for the following statements.
(i) The sum of numbers x and 4 is 9.
Solution:
The above statement can be written in the equation form as,
= x + 4 = 9
(ii) 2 subtracted from y is 8.
Solution:
The above statement can be written in the equation form as,
= y – 2 = 8
(iii) Ten times a is 70.
Solution:
The above statement can be written in the equation form as,
= 10a = 70
(iv) The number b divided by 5 gives 6.
Solution:
The above statement can be written in the equation form as,
= (b/5) = 6
(v) Three-fourths of t is 15.
Solution:
The above statement can be written in the equation form as,
= ¾t = 15
(vi) Seven times m plus 7 gets you 77.
Solution:
The above statement can be written in the equation form as,
Seven times m is 7m.
= 7m + 7 = 77
(vii) One-fourth of a number x minus 4 gives 4.
Solution:
The above statement can be written in the equation form as,
One-fourth of a number x is x/4.
= x/4 – 4 = 4
(viii) If you take away 6 from 6 times y, you get 60.
Solution:
The above statement can be written in the equation form as,
6 times y is 6y.
= 6y – 6 = 60
(ix) If you add 3 to one-third of z, you get 30.
Solution:
The above statement can be written in the equation form as,
One-third of z is z/3.
= 3 + z/3 = 30
5. Write the following equations in statement forms.
(i) p + 4 = 15
Solution:
The sum of numbers p and 4 is 15.
(ii) m – 7 = 3
Solution:
7 subtracted from m is 3.
(iii) 2m = 7
Solution:
Twice of number m is 7.
(iv) m/5 = 3
Solution:
The number m divided by 5 gives 3.
(v) (3m)/5 = 6
Solution:
Three-fifth of m is 6.
(vi) 3p + 4 = 25
Solution:
Three times p plus 4 gives you 25.
(vii) 4p – 2 = 18
Solution:
Four times p minus 2 gives you 18.
(viii) p/2 + 2 = 8
Solution:
If you add half of a number p to 2, you get 8.
6. Set up an equation in the following cases.
(i) Irfan says that he has 7 marbles, more than five times the marbles Parmit has. Irfan has 37 marbles (Take m to be the number of Parmit’s marbles).
Solution:
From the question, it is given that
Number of Parmit’s marbles = m
Then,
Irfan has 7 marbles, more than five times the marbles Parmit has.
= 5 × Number of Parmit’s marbles + 7 = Total number of marbles Irfan having
= (5 × m) + 7 = 37
= 5m + 7 = 37
(ii) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age (Take Laxmi’s age to be y years).
Solution:
From the question, it is given that
Let Laxmi’s age be = y years old
Then,
Lakshmi’s father is 4 years older than three times her age.
= 3 × Laxmi’s age + 4 = Age of Lakshmi’s father
= (3 × y) + 4 = 49
= 3y + 4 = 49
(iii) The teacher tells the class that the highest marks obtained by a student in her class are twice the lowest marks plus 7. The highest score is 87 (Take the lowest score to be l).
Solution:
From the question, it is given that
Highest score in the class = 87
Let the lowest score be l.
= 2 × Lowest score + 7 = Highest score in the class
= (2 × l) + 7 = 87
= 2l + 7 = 87
(iv) In an isosceles triangle, the vertex angle is twice either base angle (Let the base angle be b in degrees. Remember that the sum of angles of a triangle is 180 degrees).
Solution:
From the question, it is given that
We know that the sum of angles of a triangle is 180o
Let the base angle be b.
Then,
Vertex angle = 2 × base angle = 2b
= b + b + 2b = 180o
= 4b = 180o
Exercise 4.2
1. Give first the step you will use to separate the variable and then solve the equation.
(a) x – 1 = 0
Solution:
We have to add 1 to both sides of the given equation.
Then, we get
= x – 1 + 1 = 0 + 1
= x = 1
(b) x + 1 = 0
Solution:
We have to subtract 1 from both sides of the given equation.
Then, we get
= x + 1 – 1 = 0 – 1
= x = – 1
(c) x – 1 = 5
Solution:
We have to add 1 to both sides of the given equation.
Then, we get
= x – 1 + 1 = 5 + 1
= x = 6
(d) x + 6 = 2
Solution:
We have to subtract 6 from both sides of the given equation.
Then, we get
= x + 6 – 6 = 2 – 6
= x = – 4
(e) y – 4 = – 7
Solution:
We have to add 4 to both sides of the given equation.
Then, we get
= y – 4 + 4 = – 7 + 4
= y = – 3
(f) y – 4 = 4
Solution:
We have to add 4 to both sides of the given equation.
Then, we get
= y – 4 + 4 = 4 + 4
= y = 8
(g) y + 4 = 4
Solution:
We have to subtract 4 from both sides of the given equation.
Then, we get
= y + 4 – 4 = 4 – 4
= y = 0
(h) y + 4 = – 4
Solution:
We have to subtract 4 from both sides of the given equation.
Then, we get
= y + 4 – 4 = – 4 – 4
= y = – 8
2. Give first the step you will use to separate the variable and then solve the equation.
(a) 3l = 42
Solution:
Now, we have to divide both sides of the equation by 3.
Then, we get
= 3l/3 = 42/3
= l = 14
(b) b/2 = 6
Solution:
Now, we have to multiply both sides of the equation by 2.
Then, we get
= b/2 × 2= 6 × 2
= b = 12
(c) p/7 = 4
Solution:
Now, we have to multiply both sides of the equation by 7.
Then, we get
= p/7 × 7= 4 × 7
= p = 28
(d) 4x = 25
Solution:
Now, we have to divide both sides of the equation by 4
Then, we get
= 4x/4 = 25/4
= x = 25/4
(e) 8y = 36
Solution:
Now, we have to divide both sides of the equation by 8.
Then, we get
= 8y/8 = 36/8
= x = 9/2
(f) (z/3) = (5/4)
Solution:
Now, we have to multiply both sides of the equation by 3.
Then, we get
= (z/3) × 3 = (5/4) × 3
= x = 15/4
(g) (a/5) = (7/15)
Solution:
Now, we have to multiply both sides of the equation by 5.
Then, we get
= (a/5) × 5 = (7/15) × 5
= a = 7/3
(h) 20t = – 10
Solution:
Now, we have to divide both sides of the equation by 20.
Then, we get
= 20t/20 = -10/20
= x = – ½
3. Give the steps you will use to separate the variable and then solve the equation.
(a) 3n – 2 = 46
Solution:
First, we have to add 2 to both sides of the equation.
Then, we get
= 3n – 2 + 2 = 46 + 2
= 3n = 48
Now,
We have to divide both sides of the equation by 3.
Then, we get
= 3n/3 = 48/3
= n = 16
(b) 5m + 7 = 17
Solution:
First, we have to subtract 7 from both sides of the equation.
Then, we get
= 5m + 7 – 7 = 17 – 7
= 5m = 10
Now,
We have to divide both sides of the equation by 5.
Then, we get
= 5m/5 = 10/5
= m = 2
(c) 20p/3 = 40
Solution:
First, we have to multiply both sides of the equation by 3.
Then, we get
= (20p/3) × 3 = 40 × 3
= 20p = 120
Now,
We have to divide both sides of the equation by 20.
Then, we get
= 20p/20 = 120/20
= p = 6
(d) 3p/10 = 6
Solution:
First, we have to multiply both sides of the equation by 10.
Then, we get
= (3p/10) × 10 = 6 × 10
= 3p = 60
Now,
We have to divide both sides of the equation by 3.
Then, we get
= 3p/3 = 60/3
= p = 20
4. Solve the following equations.
(a) 10p = 100
Solution:
Now,
We have to divide both sides of the equation by 10.
Then, we get
= 10p/10 = 100/10
= p = 10
(b) 10p + 10 = 100
Solution:
First, we have to subtract 10 from both sides of the equation.
Then, we get
= 10p + 10 – 10 = 100 – 10
= 10p = 90
Now,
We have to divide both sides of the equation by 10.
Then, we get
= 10p/10 = 90/10
= p = 9
(c) p/4 = 5
Solution:
Now,
We have to multiply both sides of the equation by 4.
Then, we get
= p/4 × 4 = 5 × 4
= p = 20
(d) – p/3 = 5
Solution:
Now,
We have to multiply both sides of the equation by – 3.
Then, we get
= – p/3 × (- 3) = 5 × (- 3)
= p = – 15
(e) 3p/4 = 6
Solution:
First, we have to multiply both sides of the equation by 4.
Then, we get
= (3p/4) × (4) = 6 × 4
= 3p = 24
Now,
We have to divide both sides of the equation by 3.
Then, we get
= 3p/3 = 24/3
= p = 8
(f) 3s = – 9
Solution:
Now,
We have to divide both sides of the equation by 3.
Then, we get
= 3s/3 = -9/3
= s = -3
(g) 3s + 12 = 0
Solution:
First, we have to subtract 12 from both sides of the equation.
Then, we get
= 3s + 12 – 12 = 0 – 12
= 3s = -12
Now,
We have to divide both sides of the equation by 3.
Then, we get
= 3s/3 = -12/3
= s = – 4
(h) 3s = 0
Solution:
Now,
We have to divide both sides of the equation by 3.
Then, we get
= 3s/3 = 0/3
= s = 0
(i) 2q = 6
Solution:
Now,
We have to divide both sides of the equation by 2.
Then, we get
= 2q/2 = 6/2
= q = 3
(j) 2q – 6 = 0
Solution:
First, we have to add 6 to both sides of the equation.
Then, we get
= 2q – 6 + 6 = 0 + 6
= 2q = 6
Now,
We have to divide both sides of the equation by 2.
Then, we get
= 2q/2 = 6/2
= q = 3
(k) 2q + 6 = 0
Solution:
First, we have to subtract 6 from both sides of the equation.
Then, we get
= 2q + 6 – 6 = 0 – 6
= 2q = – 6
Now,
We have to divide both sides of the equation by 2.
Then, we get
= 2q/2 = – 6/2
= q = – 3
(l) 2q + 6 = 12
Solution:
First, we have to subtract 6 from both sides of the equation.
Then, we get
= 2q + 6 – 6 = 12 – 6
= 2q = 6
Now,
We have to divide both sides of the equation by 2.
Then, we get
= 2q/2 = 6/2
= q = 3
Exercise 4.3
1. Solve the following equations.
(a) 2y + (5/2) = (37/2)
Solution:
By transposing (5/2) from LHS to RHS, it becomes -5/2
Then,
= 2y = (37/2) – (5/2)
= 2y = (37-5)/2
= 2y = 32/2
Now,
Divide both sides by 2.
= 2y/2 = (32/2)/2
= y = (32/2) × (1/2)
= y = 32/4
= y = 8
(b) 5t + 28 = 10
Solution:
By transposing 28 from LHS to RHS, it becomes -28
Then,
= 5t = 10 – 28
= 5t = – 18
Now,
Divide both sides by 5.
= 5t/5= -18/5
= t = -18/5
(c) (a/5) + 3 = 2
Solution:
By transposing 3 from LHS to RHS, it becomes -3
Then,
= a/5 = 2 – 3
= a/5 = – 1
Now,
Multiply both sides by 5.
= (a/5) × 5= -1 × 5
= a = -5
(d) (q/4) + 7 = 5
Solution:
By transposing 7 from LHS to RHS, it becomes -7
Then,
= q/4 = 5 – 7
= q/4 = – 2
Now,
Multiply both sides by 4.
= (q/4) × 4= -2 × 4
= a = -8
(e) (5/2) x = -5
Solution:
First, we have to multiply both sides by 2.
= (5x/2) × 2 = – 5 × 2
= 5x = – 10
Now,
We have to divide both sides by 5.
Then, we get
= 5x/5 = -10/5
= x = -2
(f) (5/2) x = 25/4
Solution:
First, we have to multiply both sides by 2.
= (5x/2) × 2 = (25/4) × 2
= 5x = (25/2)
Now,
We have to divide both sides by 5.
Then, we get
= 5x/5 = (25/2)/5
= x = (25/2) × (1/5)
= x = (5/2)
(g) 7m + (19/2) = 13
Solution:
By transposing (19/2) from LHS to RHS, it becomes -19/2
Then,
= 7m = 13 – (19/2)
= 7m = (26 – 19)/2
= 7m = 7/2
Now,
Divide both sides by 7.
= 7m/7 = (7/2)/7
= m = (7/2) × (1/7)
= m = ½
(h) 6z + 10 = – 2
Solution:
By transposing 10 from LHS to RHS, it becomes – 10
Then,
= 6z = -2 – 10
= 6z = – 12
Now,
Divide both sides by 6.
= 6z/6 = -12/6
= m = – 2
(i) (3/2) l = 2/3
Solution:
First, we have to multiply both sides by 2.
= (3l/2) × 2 = (2/3) × 2
= 3l = (4/3)
Now,
We have to divide both sides by 3.
Then, we get
= 3l/3 = (4/3)/3
= l = (4/3) × (1/3)
= x = (4/9)
(j) (2b/3) – 5 = 3
Solution:
By transposing -5 from LHS to RHS, it becomes 5
Then,
= 2b/3 = 3 + 5
= 2b/3 = 8
Now,
Multiply both sides by 3.
= (2b/3) × 3= 8 × 3
= 2b = 24
And,
Divide both sides by 2.
= 2b/2 = 24/2
= b = 12
2. Solve the following equations.
(a) 2(x + 4) = 12
Solution:
Let us divide both sides by 2.
= (2(x + 4))/2 = 12/2
= x + 4 = 6
By transposing 4 from LHS to RHS, it becomes -4
= x = 6 – 4
= x = 2
(b) 3(n – 5) = 21
Solution:
Let us divide both sides by 3.
= (3(n – 5))/3 = 21/3
= n – 5 = 7
By transposing -5 from LHS to RHS, it becomes 5
= n = 7 + 5
= n = 12
(c) 3(n – 5) = – 21
Solution:
Let us divide both sides by 3.
= (3(n – 5))/3 = – 21/3
= n – 5 = -7
By transposing -5 from LHS to RHS, it becomes 5
= n = – 7 + 5
= n = – 2
(d) – 4(2 + x) = 8
Solution:
Let us divide both sides by -4.
= (-4(2 + x))/ (-4) = 8/ (-4)
= 2 + x = -2
By transposing 2 from LHS to RHS, it becomes – 2
= x = -2 – 2
= x = – 4
(e) 4(2 – x) = 8
Solution:
Let us divide both sides by 4.
= (4(2 – x))/ 4 = 8/ 4
= 2 – x = 2
By transposing 2 from LHS to RHS, it becomes – 2
= – x = 2 – 2
= – x = 0
= x = 0
3. Solve the following equations.
(a) 4 = 5(p – 2)
Solution:
Let us divide both sides by 5.
= 4/5 = (5(p – 2))/5
= 4/5 = p -2
By transposing – 2 from RHS to LHS, it becomes 2
= (4/5) + 2 = p
= (4 + 10)/ 5 = p
= p = 14/5
(b) – 4 = 5(p – 2)
Solution:
Let us divide both sides by 5.
= – 4/5 = (5(p – 2))/5
= – 4/5 = p -2
By transposing – 2 from RHS to LHS, it becomes 2
= – (4/5) + 2 = p
= (- 4 + 10)/ 5 = p
= p = 6/5
(c) 16 = 4 + 3(t + 2)
Solution:
By transposing 4 from RHS to LHS, it becomes – 4
= 16 – 4 = 3(t + 2)
= 12 = 3(t + 2)
Let us divide both sides by 3.
= 12/3 = (3(t + 2))/ 3
= 4 = t + 2
By transposing 2 from RHS to LHS, it becomes – 2
= 4 – 2 = t
= t = 2
(d) 4 + 5(p – 1) =34
Solution:
By transposing 4 from LHS to RHS, it becomes – 4
= 5(p – 1) = 34 – 4
= 5(p – 1) = 30
Let us divide both sides by 5.
= (5(p – 1))/ 5 = 30/5
= p – 1 = 6
By transposing – 1 from RHS to LHS, it becomes 1
= p = 6 + 1
= p = 7
(e) 0 = 16 + 4(m – 6)
Solution:
By transposing 16 from RHS to LHS, it becomes – 16
= 0 – 16 = 4(m – 6)
= – 16 = 4(m – 6)
Let us divide both sides by 4.
= – 16/4 = (4(m – 6))/ 4
= – 4 = m – 6
By transposing – 6 from RHS to LHS, it becomes 6
= – 4 + 6 = m
= m = 2
4. (a) Construct 3 equations starting with x = 2
Solution:
The first equation is,
Multiply both sides by 6.
= 6x = 12 … [equation 1]
The second equation is,
Subtracting 4 from both sides,
= 6x – 4 = 12 -4
= 6x – 4 = 8 … [equation 2]
The third equation is,
Divide both sides by 6.
= (6x/6) – (4/6) = (8/6)
= x – (4/6) = (8/6) … [equation 3]
(b) Construct 3 equations starting with x = – 2
Solution:
The first equation is,
Multiply both sides by 5.
= 5x = -10 … [equation 1]
The second equation is,
Subtracting 3 from both sides,
= 5x – 3 = – 10 – 3
= 5x – 3 = – 13 … [equation 2]
The third equation is,
Dividing both sides by 2.
= (5x/2) – (3/2) = (-13/2) … [equation 3]
Exercise 4.4
1. Set up equations and solve them to find the unknown numbers in the following cases.
(a) Add 4 to eight times a number; you get 60.
Solution:
Let us assume the required number is x.
Eight times a number = 8x
The given above statement can be written in the equation form as,
= 8x + 4 = 60
By transposing 4 from LHS to RHS, it becomes – 4
= 8x = 60 – 4
= 8x = 56
Divide both sides by 8.
Then, we get
= (8x/8) = 56/8
= x = 7
(b) One-fifth of a number minus 4 gives 3.
Solution:
Let us assume the required number is x.
One-fifth of a number = (1/5) x = x/5
The given above statement can be written in the equation form as,
= (x/5) – 4 = 3
By transposing – 4 from LHS to RHS, it becomes 4
= x/5 = 3 + 4
= x/5 = 7
Multiply both sides by 5.
Then. we get
= (x/5) × 5 = 7 × 5
= x = 35
(c) If I take three-fourths of a number and add 3 to it, I get 21.
Solution:
Let us assume the required number is x.
Three-fourths of a number = (3/4) x
The given above statement can be written in the equation form as,
= (3/4) x + 3 = 21
By transposing 3 from LHS to RHS, it becomes – 3
= (3/4) x = 21 – 3
= (3/4) x = 18
Multiply both sides by 4.
Then, we get
= (3x/4) × 4 = 18 × 4
= 3x = 72
Then,
Divide both sides by 3.
= (3x/3) = 72/3
= x = 24
(d) When I subtracted 11 from twice a number, the result was 15.
Solution:
Let us assume the required number is x.
Twice a number = 2x
The given above statement can be written in the equation form as,
= 2x –11 = 15
By transposing -11 from LHS to RHS, it becomes 11
= 2x = 15 + 11
= 2x = 26
Then,
Divide both sides by 2.
= (2x/2) = 26/2
= x = 13
(e) Munna subtracts thrice the number of notebooks he has from 50, and he finds the result to be 8.
Solution:
Let us assume the required number is x.
Thrice the number = 3x
The given above statement can be written in the equation form as,
= 50 – 3x = 8
By transposing 50 from LHS to RHS, it becomes – 50
= – 3x = 8 – 50
= -3x = – 42
Then,
Divide both sides by -3.
= (-3x/-3) = – 42/-3
= x = 14
(f) Ibenhal thinks of a number. If she adds 19 to it and divides the sum by 5, she will get 8.
Solution:
Let us assume the required number is x.
The given above statement can be written in the equation form as,
= (x + 19)/5 = 8
Multiply both sides by 5.
= ((x + 19)/5) × 5 = 8 × 5
= x + 19 = 40
Then,
By transposing 19 from LHS to RHS, it becomes – 19
= x = 40 – 19
= x = 21
(g) Anwar thinks of a number. If he takes away 7 from 5/2 of the number, the result is 23.
Solution:
Let us assume the required number is x
5/2 of the number = (5/2) x
The given above statement can be written in the equation form as,
= (5/2) x – 7 = 23
By transposing -7 from LHS to RHS, it becomes 7
= (5/2) x = 23 + 7
= (5/2) x = 30
Multiply both sides by 2,
= ((5/2) x) × 2 = 30 × 2
= 5x = 60
Then,
Divide both sides by 5.
= 5x/5 = 60/5
= x = 12
2. Solve the following.
(a) The teacher tells the class that the highest marks obtained by a student in her class are twice the lowest marks plus 7. The highest score is 87. What is the lowest score?
Solution:
Let us assume the lowest score is x.
From the question, it is given that
The highest score is = 87
The highest marks obtained by a student in her class are twice the lowest marks plus 7= 2x + 7
5/2 of the number = (5/2) x
The given above statement can be written in the equation form as,
Then,
= 2x + 7 = Highest score
= 2x + 7 = 87
By transposing 7 from LHS to RHS, it becomes -7
= 2x = 87 – 7
= 2x = 80
Now,
Divide both sides by 2.
= 2x/2 = 80/2
= x = 40
Hence, the lowest score is 40.
(b) In an isosceles triangle, the base angles are equal. The vertex angle is 40°. What are the base angles of the triangle? (Remember, the sum of three angles of a triangle is 180°.)
Solution:
From the question, it is given that
We know that the sum of angles of a triangle is 180o
Let the base angle be b.
Then,
= b + b + 40o = 180o
= 2b + 40 = 180o
By transposing 40 from LHS to RHS, it becomes -40
= 2b = 180 – 40
= 2b = 140
Now,
Divide both sides by 2.
= 2b/2 = 140/2
= b = 70o
Hence, 70o is the base angle of an isosceles triangle.
(c) Sachin scored twice as many runs as Rahul. Together, their runs fell two short of a double century. How many runs did each one score?
Solution:
Let us assume Rahul’s score is x.
Then,
Sachin scored twice as many runs as Rahul is 2x.
Together, their runs fell two short of a double century.
= Rahul’s score + Sachin’s score = 200 – 2
= x + 2x = 198
= 3x = 198
Divide both sides by 3.
= 3x/3 = 198/3
= x = 66
So, Rahul’s score is 66.
And Sachin’s score is 2x = 2 × 66 = 132
3. Solve the following:
(i) Irfan says that he has 7 marbles, more than five times the marbles Parmit has. Irfan has 37 marbles. How many marbles does Parmit have?
Solution:
Let us assume the number of Parmit’s marbles = m
From the question, it is given that
Then,
Irfan has 7 marbles, more than five times the marbles Parmit has.
= 5 × Number of Parmit’s marbles + 7 = Total number of marbles Irfan having
= (5 × m) + 7 = 37
= 5m + 7 = 37
By transposing 7 from LHS to RHS, it becomes -7
= 5m = 37 – 7
= 5m = 30
Divide both sides by 5.
= 5m/5 = 30/5
= m = 6
So, Permit has 6 marbles.
(ii) Laxmi’s father is 49 years old. He is 4 years older than three times Laxmi’s age. What is Laxmi’s age?
Solution:
Let Laxmi’s age be = y years old
From the question, it is given that
Lakshmi’s father is 4 years older than three times her age.
= 3 × Laxmi’s age + 4 = Age of Lakshmi’s father
= (3 × y) + 4 = 49
= 3y + 4 = 49
By transposing 4 from LHS to RHS, it becomes -4
= 3y = 49 – 4
= 3y = 45
Divide both sides by 3.
= 3y/3 = 45/3
= y = 15
So, Lakshmi’s age is 15 years.
(iii) People of Sundargram planted trees in the village garden. Some of the trees were fruit trees. The number of non-fruit trees was two more than three times the number of fruit trees. What was the number of fruit trees planted if the number of non-fruit trees planted was 77?
Solution:
Let the number of fruit trees be f.
From the question, it is given that
3 × number of fruit trees + 2 = number of non-fruit trees
= 3f + 2 = 77
By transposing 2 from LHS to RHS, it becomes -2
=3f = 77 – 2
= 3f = 75
Divide both sides by 3.
= 3f/3 = 75/3
= f = 25
So, the number of fruit trees was 25.
4. Solve the following riddle.
I am a number,
Tell my identity!
Take me seven times over
And add a fifty!
To reach a triple century
You still need forty!
Solution:
Let us assume the number is x.
Take me seven times over and add a fifty = 7x + 50
To reach a triple century you still need forty = (7x + 50) + 40 = 300
= 7x + 50 + 40 = 300
= 7x + 90 = 300
By transposing 90 from LHS to RHS, it becomes -90
= 7x = 300 – 90
= 7x = 210
Divide both sides by 7.
= 7x/7 = 210/7
= x = 30
Hence, the number is 30.

